Over the last couple of years, the team at La Salle Education has been thinking about assessment without levels.

National Curriculum Levels served a purpose in their original guise – a way of suggesting that mathematics is an interconnected subject, where the learning of a concept rests firmly on the foundations of earlier concepts, which must be secure before moving on.  Levels, in a very broad sense, drew a picture of what this progression might look like and suggested a pathway through mathematics as a child learned more and more.

There is nothing at all wrong with this idea.  In mathematics in particular, not only is it a correct assertion, but it is a very useful one too.  Ensuring that a student has secured underlying concepts before trying to build on top of them is the best way of giving them the chance to really learn mathematics and be successful.

Levels, in their original format, also did a good job at showing interconnections across strands of mathematics – showing that, say, some statistics should not be encountered before the underlying number work.

The abolition of National Curriculum Levels was due to a multitude of reasons, many of them ideological and many of them ignorant of the differences in subject areas.  But there were also several good reasons for their scrapping.  National Curriculum Levels, as with any metric in a high-stakes system, was an idea almost doomed to abuse at its inception.  In no time at all, because of a desperate need to ‘measure progress’, the levels were subdivided and misinterpreted.  Suddenly, the once broad and general pathway through mathematics became an ill-informed and utterly ridiculous statement of mathematics learning that simply ignored the way in which mathematics learning happens. The notion that a child can be a Level 4b in mathematics is nonsensical.  What on earth does it mean?

This is a far cry from what Level 4 was supposed to mean – a broad statement of an approximate place on a journey of learning mathematics.

Then, with such predictability, we started to see the granularity become more and more extreme.  The idea that a single test could tell you the level of a child or, worse still, that a single lesson with perhaps just one activity could brand a child with an extremely specific level.  Even a 20 minute lesson observation was starting to demand an assessment of each child’s level.

One other issue with National Curriculum Levels is that they had become a fundamentally dishonest measures.  With a fairly obscure language, it became easy for parents to misinterpret the true meaning of the metrics.  A parent told that their child has achieved Level 3, when last year their child was just Level 2, might well be pleased and feel that all is well.  But what if that child is 14 years old?  Levels all too easily disguise low attainment because they can be used to exclusively highlight progress.

At La Salle, a group of around 30 people have been constructing an assessment system with two overarching aims.  Firstly, the metric should be honest and show not only progress but attainment also.  It should give a clear indication of a trajectory so that everyone (teacher, student and parent) can play a part in intervention as soon as it is required.  Secondly, the system should reinstate the correct intentions of the Levels system – that is to say, the system should give clear guidance of a pathway through mathematics, where concepts underpin each other and the journey through an interconnected mathematics curriculum is one that gives the best possible chance of success.

We have experimented with the ideas over a couple of years.  The team is made up of a wide variety of people, from those of us who created things like the NCETM self-evaluation tool or were part of creating national programmes of study, or members of the team who are currently working in schools of various types and circumstances, to colleagues who write assessment materials for awarding bodies.  We have debated long and hard, tried various ideas and consulted with lots of teachers (and continue to do so).

The emerging result is MathsAge.

The early version of this system is already incorporated into Complete Mathematics and, as with every aspect of our work, we will continue to research and refine.  You can imagine, as more and more students interact with the system and more and more teachers give feedback, the metric can be honed and continually made more rigorous.

So what did we do?  Initially, our work centered around curriculum design and then learning design rather than assessment.  All too often, assessment is allowed to drive curriculum and learning design – this is something we have no interest in.  Curriculum and learning come first.  This meant spending years creating a journey through school age mathematics from counting to calculus.  There were many iterations of this curriculum.  The result – a progressive journey through mathematics based on the fundamental principle of securing concepts before building on top of them – is, of course, not the only pathway.  There are many areas of school age mathematics that are axiomatic, which means that there are many entry points to starting particular strands of the journey.  Nevertheless, we wanted to put in place a journey that does work – not a unique journey – but one that will work if followed.

This curriculum design then led to the most extensive piece of work: learning design.  We have been working on this for a while, with a very large team, and will continue to work on it for years to come (forever in fact), with every single teacher in Complete Mathematics also able to add to the design and debate.

Combined, these two areas of our work produced a framework - not unlike a neural network when we draw it out on paper!  This gives us a way of identifying key signposts along the journey and dividing the journey in a practical and sensible way.

The obvious response is to work with what works for schools.  So we took the full journey and divided it into 11 very broad steps, going from counting to early calculus.  The idea being that any student who successfully passes through the 11 steps will be able to achieve a Grade 9 at GCSE.

These steps contain broad statements of attainment, showing the areas that must be secure before moving on.  It does not mean that the mathematical topic will never be encountered again, but simply that there are stages in strands / topics / concepts that need to be addressed at certain points along the journey.

Why did we choose age rather than stage?  It would be easy, of course, to use the 11 steps to say ‘this is what stage you have reached on the journey’, but we wanted the metric to be really honest, particularly for parents.  So each stage is related to an age and that is what we communicate back.

It is nonsense to say a child is, for instance, a low age 12 because areas in the broad step will mature in different ways.  So we make no judgment about this sort of granular level.  Instead, and this is where the assessment design phase really kicked in, we are more interested in the ‘strength’ of the measure.  Any interaction might result in a judgment being made, but how robust is that judgment and how reliably can a teacher alter their planning?  That is our focus.  So the MathsAge comes with a ‘strength’ measure.  This will become more and more accurate as the child provides more and more evidence.

Unlike most systems available for maths education, Complete Mathematics is not a static system, which means that all of this work will continue to evolve based on real users’ interactions and real teachers’ observations and feedback.  This means that the trajectory measure will become ever more accurate.  In the meantime, the trajectory (the system is predicting what final GCSE grade a child of any age will achieve at the end of school) is underpinned by the statistics collected at national level over the last couple of decades, which give fairly accurate probability distributions of where a child will progress to given their current attainment.  We have used these probabilities as the starting point, which can then be tested over time as real children progress through the age groups.

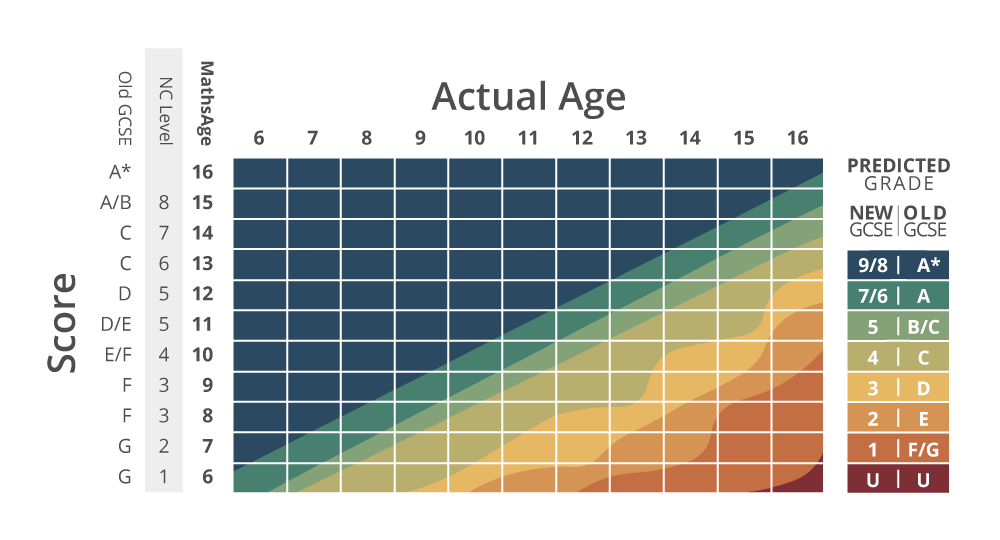
MathsAge is therefore a way of allowing everyone involved – teachers, pupils and parents – to have a clear picture of where the pupil is right now and where the pupil is heading.

Because the Complete Mathematics curriculum was the starting point, knowing a pupil’s MathsAge also allows us to know precisely which concepts are holding them back. This will give schools the ability to change their planning or to provide meaningful intervention, rather than generic booster sessions.